[신호시스템] 1. Continuous-Time Signals

Signal?

 

신호(Signal)는 수치화할 수 있는 모든 물리량이다. 신호에는 Continuous-Time Signals(연속시간신호)와 Discrete-Time Signals(이산시간신호)가 있다. ex) 주식

 

 

 

1.1 Continuous-Time Signals

 

연속시간함수(Continuous-Time Signals)는 x(t)로 표현한다. 변수 t에 대한 신호가 x라는 것이다. 즉, 신호 x는 시간 t(연속시간, 단위 : sec)에 따라 변한다. Countinous-Time Signals 와 Analog Sinal은 같은 말이다.

 

<출처>wikipedia.com Fourier analysis

1.1.1 Step and Ramp Functions

 

Continuous-Time Signals 의 대표적인 예가 unit-step function(단위계단함수) u(t)와 unit-ramp function(단위램프함수) r(t)이다. 그래프는 아래와 같다.

Unit-Step Function <출처> Fundamentals of Signals and Systems(Edward W.Kamen Bonnie S Heck)

Unit은 단위, 즉, 1이란 뜻이다. Unit-Step Function은 t가 0이상일 때, 진폭(amplitude)가 1이라는 것을 의미한다. 만약 K를 임의의 0이 아닌 실수라고 한다면, Ku(t)는 t가 0이상일 때 진폭이 K라는 것을 뜻한다. 만약에 다른 continuous-time signals x(t)와 u(t)를 곱하여 x(t)u(t)를 만들었다고 하자. t가 0이상인 부분은 x(t)가 가지고 있던 값을 그대로 가지고 오고, t가 0보다 작은 부분은 모두 0이 된다.

Unit-Ramp Function <출처> Fundamentals of Signals and Systems(Edward W.Kamen Bonnie S Heck)

ramp는 영어로 경사로라는 뜻이다. Unit-Ramp Function에서는 그래프가 경사진 모습을 보여준다. t가 0 이상인 부분에서 기울기가 1이다. 만약 K를 임의의 0이 아닌 실수라고 한다면, Kr(t)는 t가 0 이상인 부분에서 K인 기울기를 갖는다.

u(t)를 적분하면 r(t)가 나온다. u(t)는 t가 커질수록 넓이가 일정하게 증가하므로 기울기가 1인 r(t)가 나오는 것이다. 반대로 r(t)를 미분하면, 미분정의가 되지 않는 t=0을 제외한 u(t)가 나온다.

 

 

1.1.2 The Impulse

The impulse = Delta Function = Dirac ditribution. 다 같은 말이다. 한국어로는 충격함수라고도 한다. impulse는 해석하면 반응을 불러 일으키는 '충격'을 뜻한다.

 

t가 0이 아닐 때는 δ(t)가 0이지만, 충격(그래프가 올라간 부분)을 기준으로 아래 면적은 항상 1(단위면적)이다. 중요한 것은 δ(t)에서 t=0일 때, δ(0)의 값이 정의 되지 않는다. 특히, δ(0)는 무한한 값이 아니다. A가 무한히 큰 양수 값일 때, 진폭A의 값에 근접한 것이지, 무한한 것은 아니다. 임의의 숫자 K가 존재할 때, Kδ(t) 는 영역 K를 갖고 있는 충격함수이다.

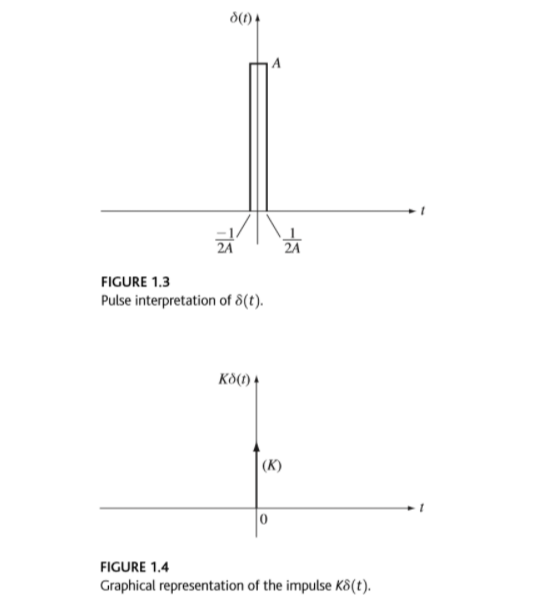
<출처> Fundamentals of Signals and Systems(Edward W.Kamen Bonnie S Heck)

u(t)함수는 δ(t)를 적분한 것과 같다. 미분 불가능한 t=0인 것을 제외할 경우다.

 

 

 

Periodic Signals

 

Periodic Signals은 주기성을 갖고 있는 신호다. 즉, 같은 값이 일정한 간격(period)을 가지고 반복되는 신호이다. 만약 continuous-time signal x(t)가 주기성을 갖고 있다면, -∞<t<∞ 범위에서 x(t+T) = x(t)라는 식이 성립된다. 주기성을 기준으로 두가지 질문을 할 수 있다.

 

①같은 값이 몇 초 간격으로 나타나는가? >> 이 문제의 답은 T초. 이 때 T는 "주기(Period)"가 되고 단위는 [sec]이다.

②같은 값이 1초에 몇 번 나타나는가? >> 이 문제의 답은 1/T회. 이 때 1/T은 "주파수(Frequency)"이고 단위는 [1/sec = Hz]이다. 즉, 주파수 f는 시간의 역수인 1/T[Hz]이다.

 

★중요하다★

 

Sinusoid(정현파)에서도 주기, 주파수, 각주파수를 볼 수 있다. Amplitude(진폭)은 A, frequency(주파수)는 f이고 T = 1/f이다. Angular frequency에서 w=2πf 이므로 이를 방금 나온 T = 1/f에 대입하면 정현파의 주기 T=2π/w이다. Phase(위상)은 θ이다. 아래 그래프에서 주기 T는 주기의 각 X 절편의 거리와 같다.(아래식 참고)

<출처> Fundamentals of Signals and Systems(Edward W.Kamen Bonnie S Heck)

 

Time-Shifted Signals

Time-Shifted Signals은 말 그대로 시간을 옮긴 신호이다. x(t)에서 x축은 시간인데, 시간축에서 평행이동을 한 것이다. 오른쪽으로 평행이동을 하면 시간이 지연된 것이고, 왼쪽으로 평행이동을 하면 시간을 거슬러 올라간 것이다. 보통 선행이라고 하는데, 수학적으로는 가능하나 물리적으로 존재하지는 않는다.

Continuous-Time Signals vs. Continuous Signal

시간이 연속인 신호가 있고 신호가 연속인 함수가 있다. 위에서 본 신호들은 시간과 신호 모두 연속이다. 하지만 신호에서 불연속점이 있다면(그래프에서 t=0인 지점이 뚫려 있다던가..) 시간은 연속이나 신호는 연속이지 않다. 보통 시간축이 t이면 연속시간이다. 이 강의에선 대부분의 시간연속신호가 연속신호이다.